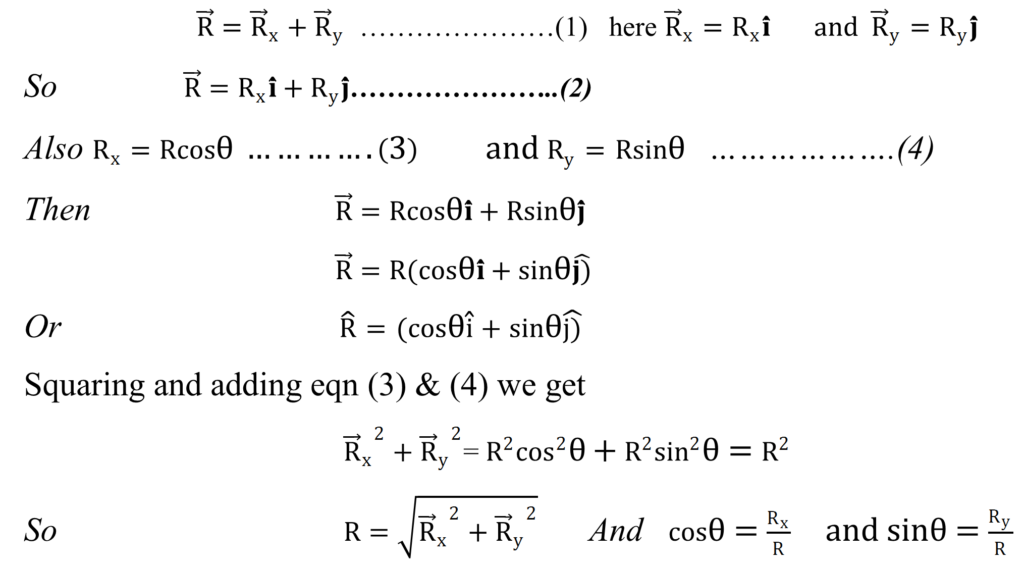Chapter–4: Motion in a Plane class 11 physics notes
Motion in a Plane Scalar and vector quantities; position and displacement vectors, general vectors and their notations; equality of vectors, multiplication of vectors by a real number; addition and subtraction of vectors, relative velocity, Unit vector; resolution of a vector in a plane, rectangular components, Scalar and Vector product of vectors.
Motion in a plane, cases of uniform velocity and uniform acceleration-projectile motion,
uniform circular motion.
2(C) PROJECTILE MOTION:-
18 PROJECTILE MOTION
A projectile is the name given to a body which once thrown upward with some initials velocity moves only under the effect of gravity alone.
The path followed by the particle is called trajectory.
E,g:- (i) A bullet fired from a rifle.
(ii)- A stone thrown horizontally from the top of a building.
QUESTION 16: What do you mean by principal of physical independence of motions?
In the absence of air a particle projected followed two motions, motion in horizontal direction and motion in vertical direction. Both the motion in horizontal direction & in vertical direction are independent on each other. This is called principle of physical independence. E,g:- if two balls dropped from the top of a building one in horizontal direction & one in vertical direction will reach the ground in same time but with different positions.
- ASSUMPTION USED IN PROJECTILE MOTION:-
(I)-there is no air resistance on the projectile.
(ii)-The effect due to curvature of earth is negligible.
(iii)The effect due to rotation of earth is negligible.
(iv)The acceleration due to gravity is constant for throughout motion.
- PROJECTILE GIVEN HORIZONTAL PROJECTION:-
Suppose a body is projected horizontally with initial velocity u from a point O at a certain height h from the ground. The body is under the influence of two simultaneously independent motions.
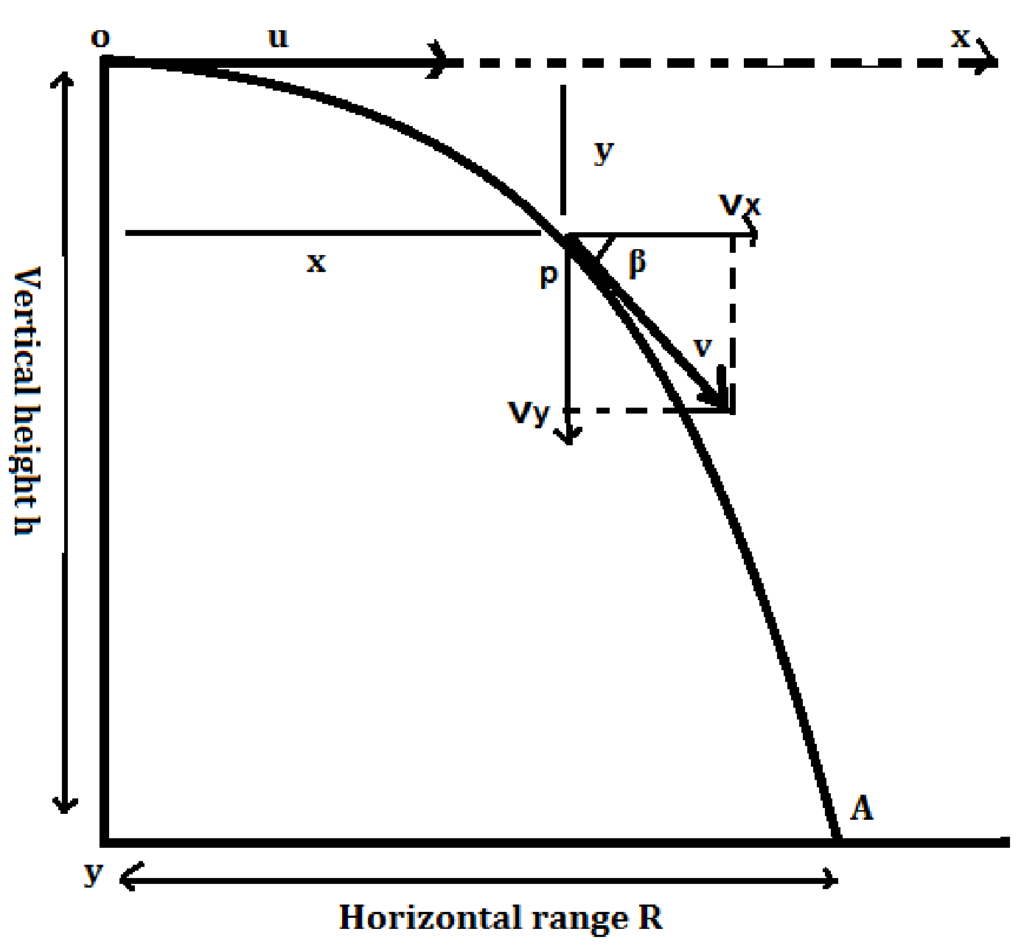
(i)- Uniform horizontal motion with velocity u.
(ii)- Vertically downwards motion with acceleration g. Under the combined effect of these two motions body moves along OPA.
(a)TRAJECTORY OF THE PROJECTILE:-
Let after the time t the body reaches the point p (x, y).
The horizontal distance covered by the body in t time is ![]()
The vertical distance travelled by the body in t time is given by
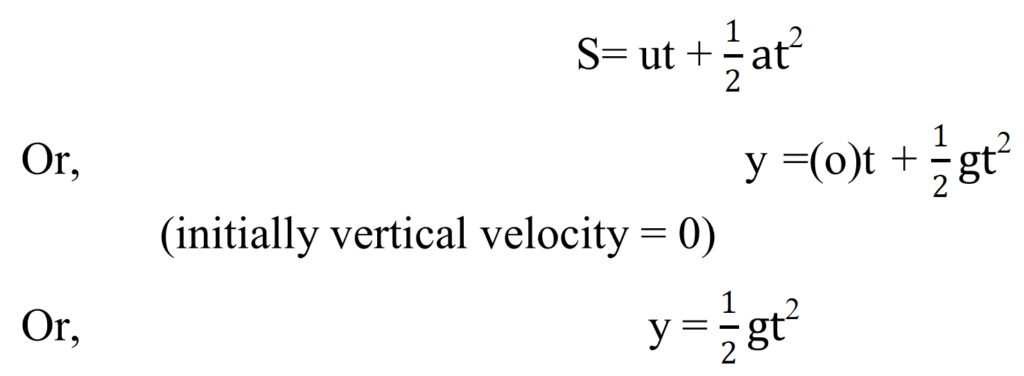
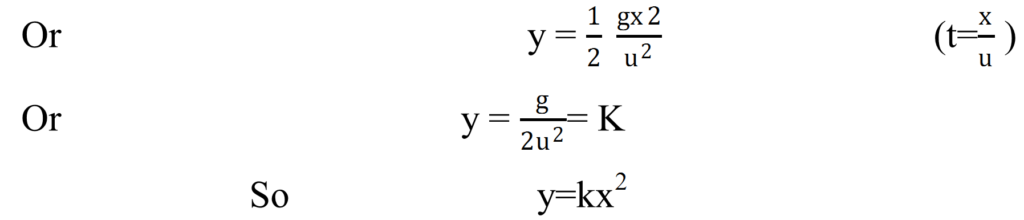
This is the eqn of parabola. Hence the particle will follow parabolic path.
(a)TIME OF FLIGHT:-
The time for which a particle or projectile remains in space is called time of flight. Let t be the time of flight.
For the vertical downward motion we have
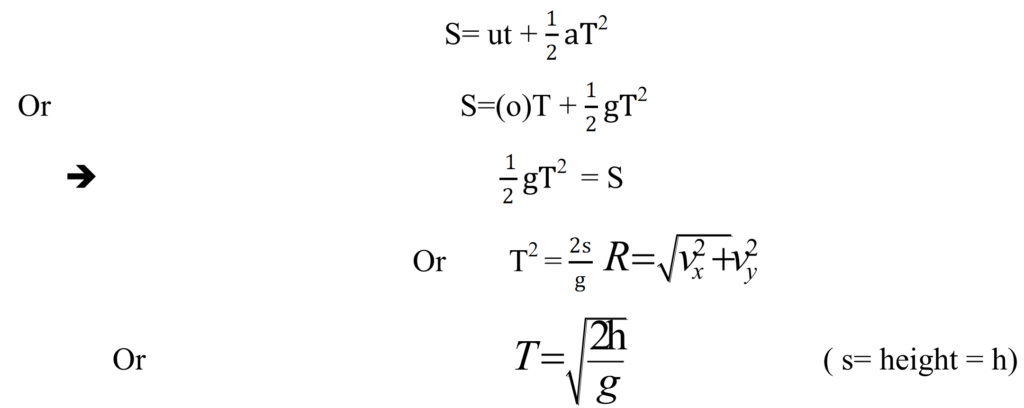
(b)HORIZONTAL RANGE:-
It is the horizontal distance covered by the projectile during its time of flight. It is equal to OA = R.
R= horizontal velocity x time of flight

VELOCITY OF THE PROJECTILE AT ANY INSTANT:-
Let v is the velocity of projectile at any instant of time. It may be divided into two components.
- Horizontal component vx = u
- Vertical component vy = 0+ gt = gt
So, the resultant velocity at point P is ![]()
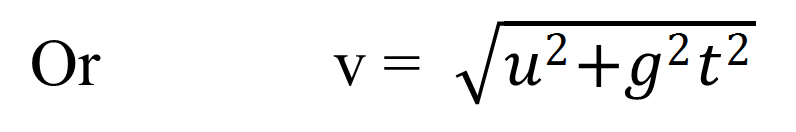
If the velocity v makes an angle β with the horizontal than
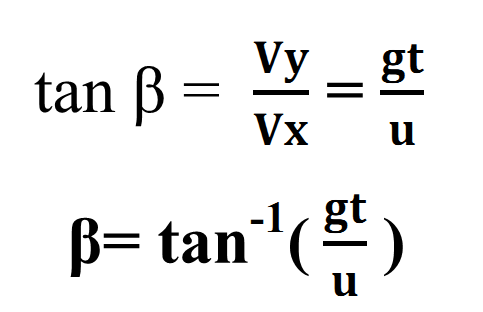
- PROJECTILE GIVEN ANGULAR PROJECTION:-Projectile fired at an angle Ѳ with the Horizontal.:-
Suppose a body is projected with initial velocity u making an angle Ѳ with the horizontal. This velocity has two rectangular components
- ucosθ along horizontal x axis.
- usin θ along vertical y axis.
Under the combined effect of above two components the body will follow the OAB path. As shown in fig.
EQUATION OF TRAJECTORY OF A PROJECTILE:-
Supose at time t the body reaches the point P (x, y). The horizontal distance covered by the body is

Which is also a trajectory of parabolic hence particle given angular projection will follow parabolic path.
TIME OF MAXIMUM HEIGHT:-
The time taken by the projectile to reach the maximum height is called time of maximum height.
As at the highest point vertical component of the velocity=0
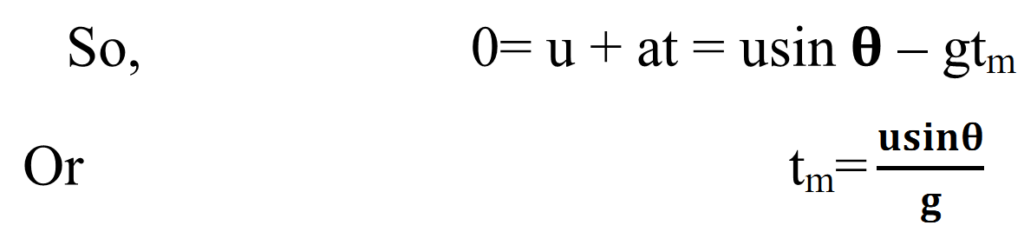
TIME OF FLIGHT:-
It is the total time for which a projectile remains in air. Net vertical displacement covered by the projectile during time of flight= 0.
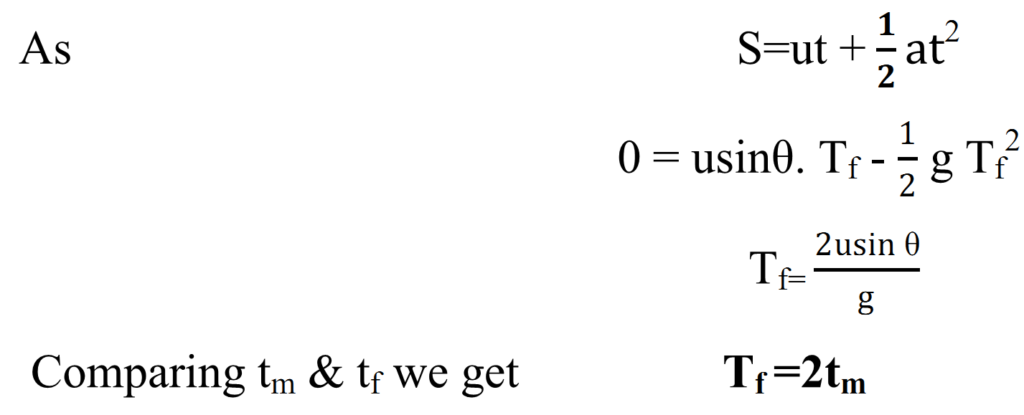
MAXIMUM HEIGHT OF THE PROJECTILE:-
The maximum vertical distance covered by the projectile is called maximum height of the projectile.
At the vertical height A, vertical component of velocity = 0

HORIZONTAL RANGE (R):-
It is the Horizontal distance travelled by the projectile during its time of flight. So,
Horizontal range = Horizontal velocity × time of flight
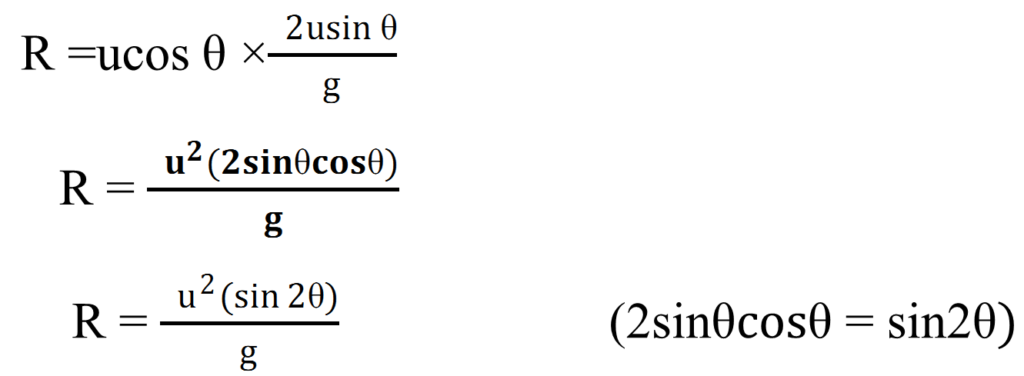
* Condition for maximum horizontal range
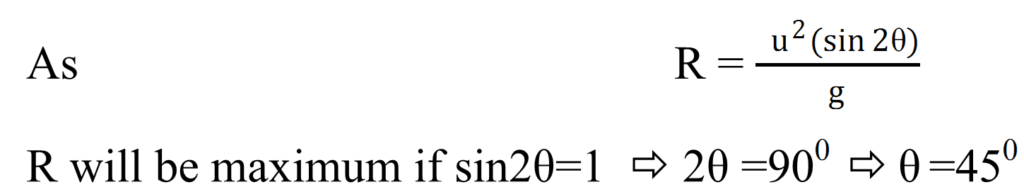
Thus if a projectile fired at 450will have maximum horizontal range & the maximum horizontal range can be given as 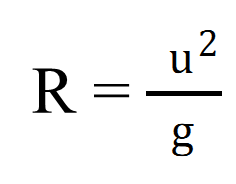
- TWO ANGLE OF PROJECTION FOR THE SAME HORIZONTAL RANGE:-
The Horizontal range of a projectile projected at an angle with the horizontal with velocity u is given by
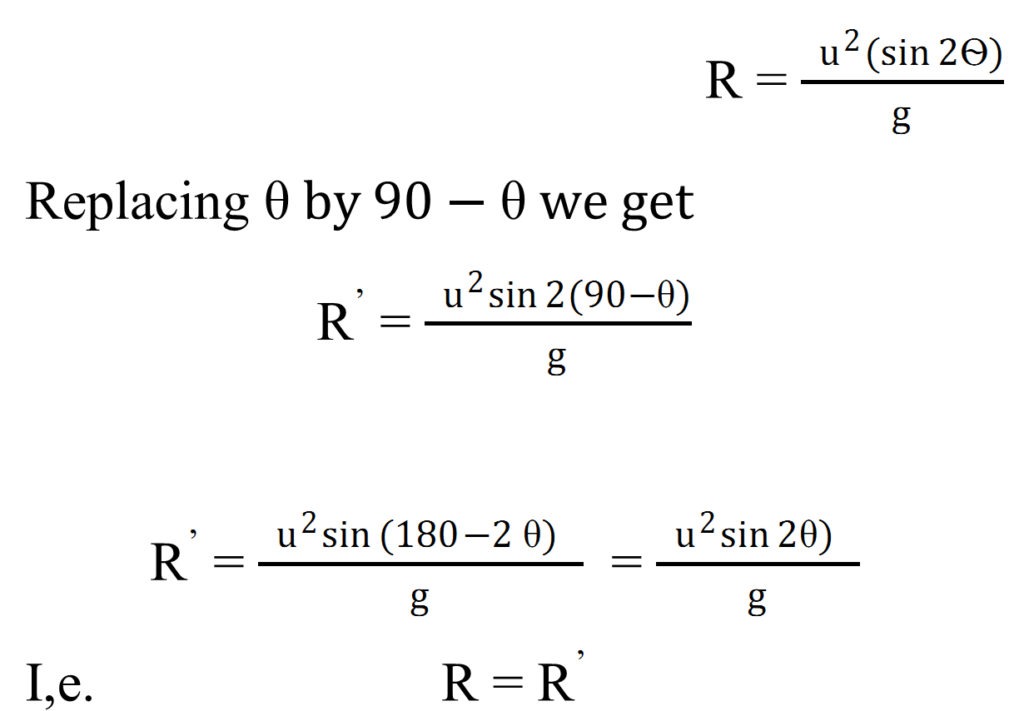
Hence for a given velocity of the projection, a projectile has same horizontal range for the angle of projection![]() Its value is maximum for
Its value is maximum for ![]()
QUESTION 16: A ball is thrown from a field with a speed of 12.0 m/s at an angle of 45° with the horizontal. At what distance will it hit the field again ? Take g = 10.0 m/s.
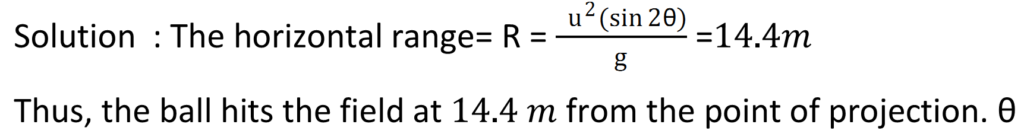
- VELOCITY OF PROJECTILE AT ANY INSTANT:-
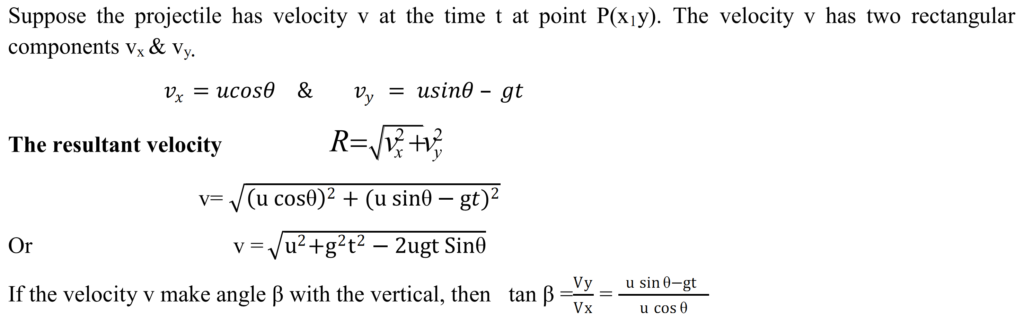
- VELOCITY OF THE PROJECTILE AT THE END POINT:-

Here –ve sign shows that the direction is downward. Hence Projectile returns to ground at the same angle at which it is fired.
QUESTION 17: A football is kicked with a velocity of 20 m/s at an angle of 45° with the horizontal. (a) Find the time taken by the ball to strike the ground. (b) Find the maximum height it reaches. (c) How far away from the kick does it hit the ground ? Take g = 10 m/s 2.

2(D) Scalar and Vectors
- PHYSICAL QUANTITY
In the study of the two dimensional motion of the physical quantity we need sometime both magnitude and the direction of the quantity so introduced a new term vector.
A physical quantity may be divided into two types
Scalar Quantity:-
Physical quantities that have only magnitude and no direction are called scalar quantities or scalars. Eg: mass, time, speed etc.
Vector Quantity:-
Physical quantities that have both magnitude and direction are called vector quantities or vectors. Eg: displacement, weight, velocity, force etc.
Difference between scalar and vector quantity
| Scalar quantity | Vector quantity |
| 1.Scalar quantity have only magnitudes | 1.Vector quantity have both magnitude and direction |
| 2.Scalar quantity changes when magnitude of the quantity changes | 2.Vector quantity changes when either magnitude or direction changes |
| 3.Scalar can be added by the ordinary laws of the algebra | 3.Vectors can be added by only special laws of vector addition |
- . Representation of vectors A vector is represented by using a straight line with an arrowhead at one end. The length of the line represents the magnitude of the vector and the arrowhead gives its direction.

26.. Types of vectors
Equal vectors:-Vectors are said to be equal if they have the same magnitude and same direction.

Negative vector A vector having the same magnitude but direction opposite to that of a given vector is called negative vector of the given vector.

.Unit vector A vector whose magnitude is unity (one) is called a unit vector. It is represented as
As 
Unit vector have direction as same as its parent atom.
Orthogonal unit vectors:-
three mutually perpendicular vectors ![]() are called orthogonal unit vectors.
are called orthogonal unit vectors.
These vectors may be represented as 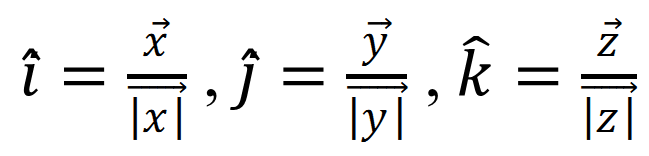
Zero vector or null vector:-
It is a vector, which has zero magnitude and an arbitrary direction. It is represented by ![]()
.when a vector is added to zero vector then we get the same vector as ![]()
When a real number or a vector is multiplied to zero vectors then we get the zero vector![]()
If![]() and μ are two none zero real numbers then the relation
and μ are two none zero real numbers then the relation ![]() can hold only when both
can hold only when both
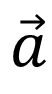 are
are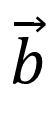 zero vectors.
zero vectors.polar vector :-
The vectors which have starting point are called polar vectors like displacement vector, force etc.
Axial vector:-
the vectors which represents the rotational effect and act always along the axis of rotation in accordance with the right hand screw rule are called axial vector. For example angular velocity, torque, angular momentum etc.
Position Vector:
The position vector is used to specify the position of a certain body. The position vector of an object is measured from the origin, in general. Suppose an object is placed in the space as shown:
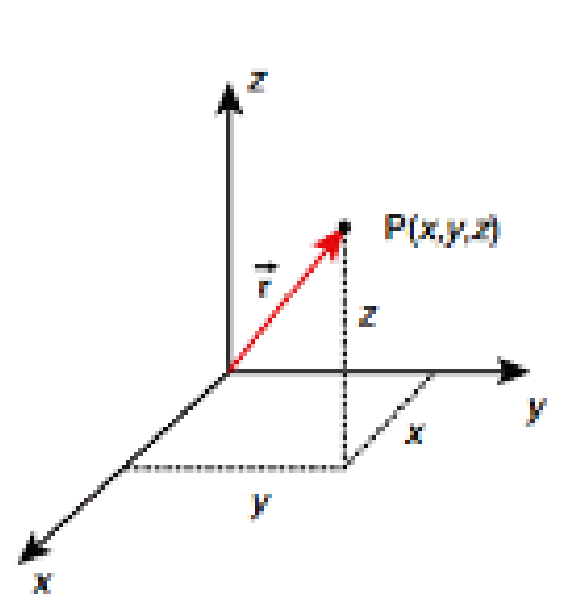
Position vector ![]()

So if an object is at a certain point P (say) at a certain time, its position vector is given as described above.
Displacement Vector:
The change in the position vector of an object is known as the displacement vector. Suppose an object is at point A at time t= 0 and at point B at time t= t. The position vectors of the object at point A and at point B are given as:
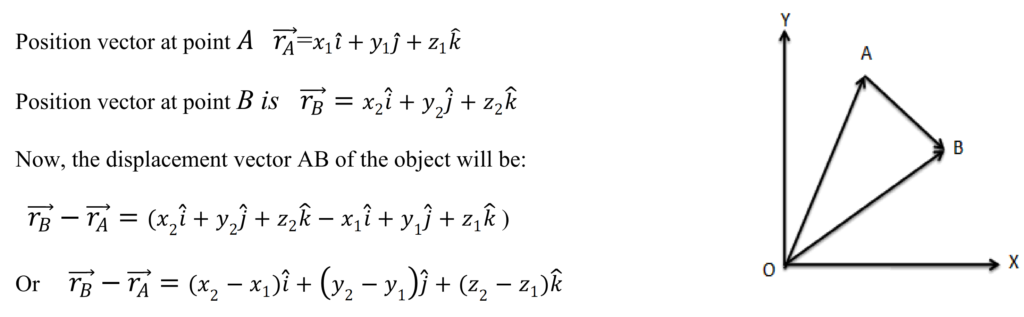
The displacement of an object can also be defined as the vector distance between the initial point and the final point. Suppose an object travels from point A to point B in the path shown in the black curve:
- Addition of vectors.
- When the vectors are in the same direction.
Here the magnitude of the resultant vector is equal to the sum of the magnitudes of the two vectors and direction is same as that of the two vectors.
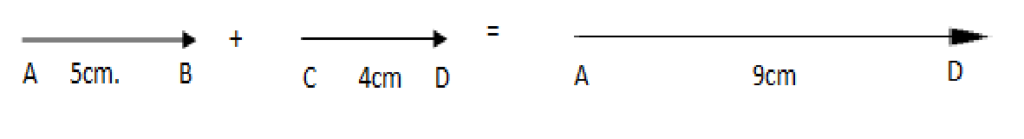
- When the vectors are in opposite directions.
Here the magnitude of the resultant is the difference in magnitude of the two vectors and the direction is same as that of the bigger vector.

- When the vectors are inclined at an angle.
When the vectors are inclined at an angle, the sum of vectors can be determined using two methods:
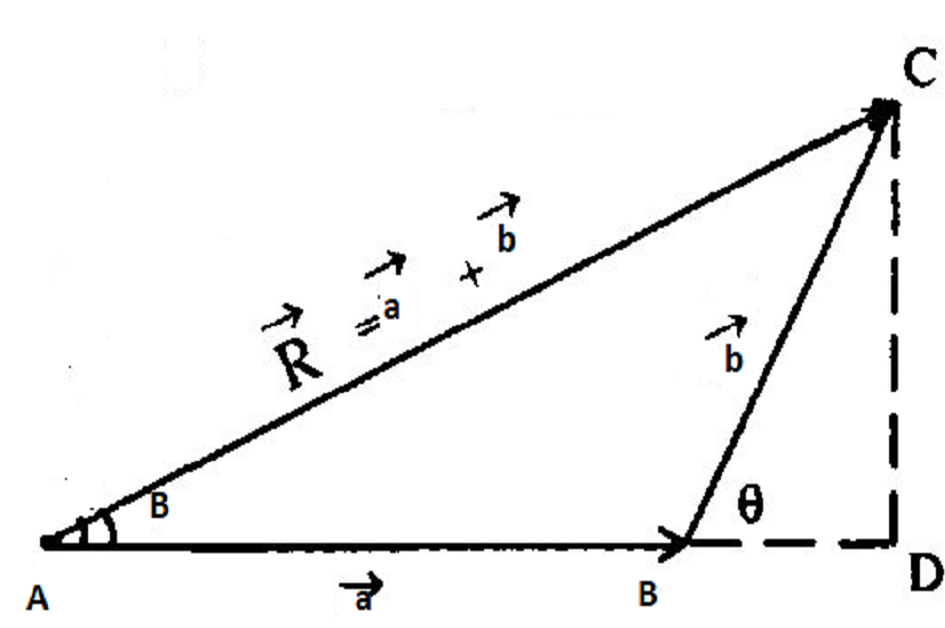
(a) Triangle law of vectors:
“If two vectors are represented by the two sides of a triangle, both in magnitude and in direction, and in same order, then the third side of the triangle in the reverse order represents the vector sum of the vectors.”
I.e. ![]()
Magnitude of R
As shown in fig. AB and BC are two vectors taken in the same order and AC is the vector taken in the opposite order. Now to obtain the magnitude of vector R draw CD perpendicular to AD then from the triangle ACD
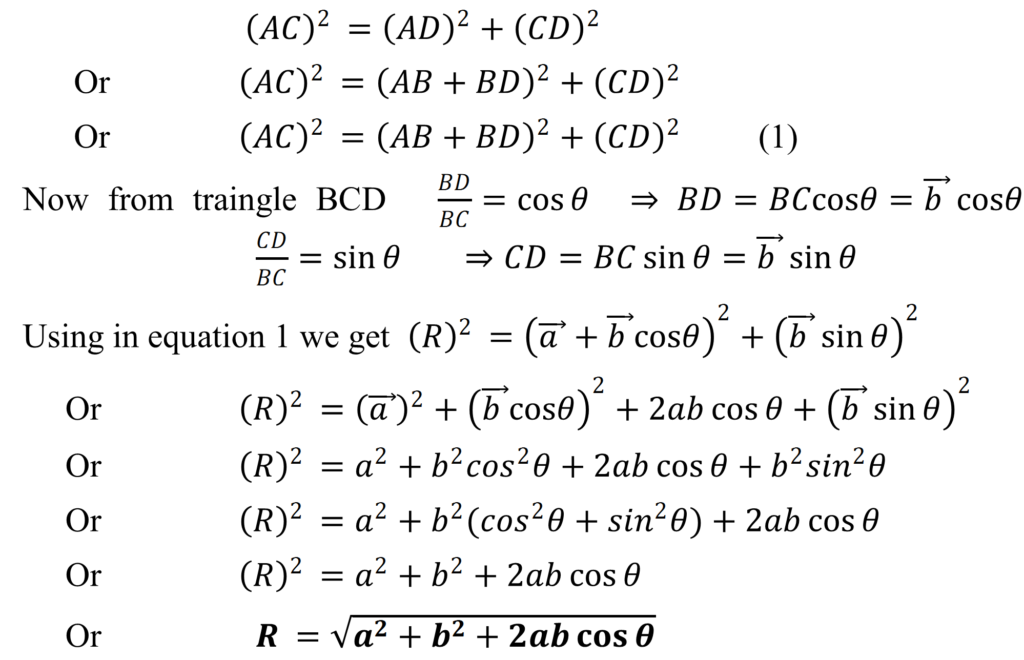
Which is the required expression for the magnitude of the ![]() .
.
Direction of the ![]()
The direction of the resultant vector can be given by the slope of the resultant or we can say by the
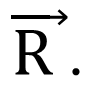
As from the diagram
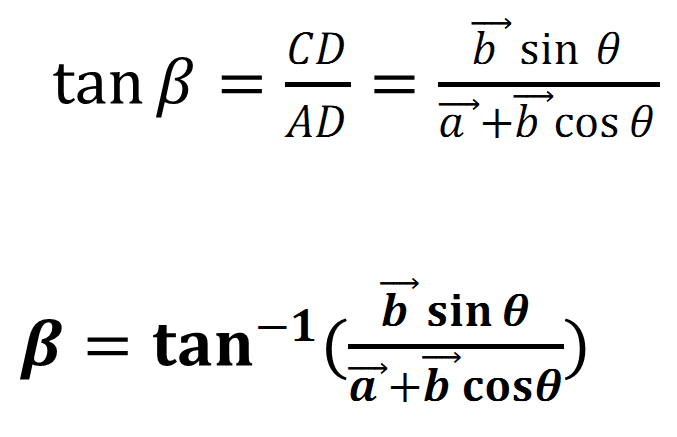
QUESTION 18: Two vectors of equal magnitude 5 unit have an angle 60° between them. Find the magnitude of (a) the sum of the vectors and (b) the difference of the vectors.

(b) Parallelogram law of vectors.
“If two vectors are represented both in magnitude and in direction by the adjacent sides of a parallelogram, then the diagonal of the parallelogram starting from the point of intersection of the two vectors represent the vector sum of the two vectors”.
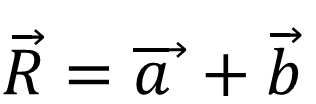
suppose AB and AE are the two vectors representing as the two adjacent sides of a parallelogram. AC is the greater diagonal of parallelogram. Now draw CD perpendicular to AD. then from the triangle ACD

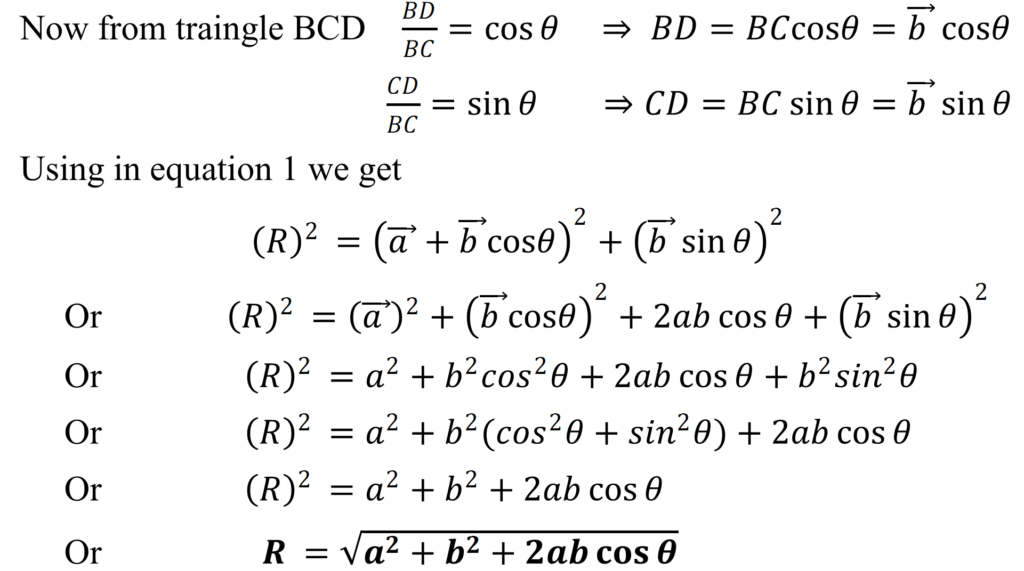
Which is the required expression for the magnitude of ![]() .
.
Direction of the ![]()
The direction of the resultant vector can be given by the slope of the resultant or we can say by the
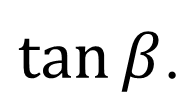 As from the diagram
As from the diagram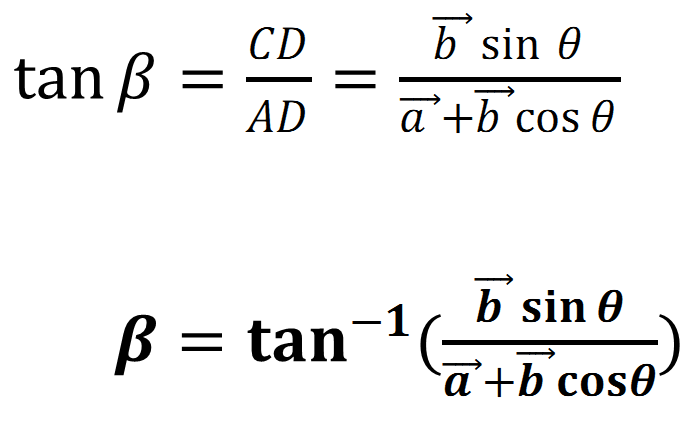
(c )Polygon law of vector addition:-
According to the polygon law of vector addition, if a number of the vectors represent the sides of a open polygon
taken in same order then their resultant vector is represented by the closed side of the polygon taken in the opposite order.
Suppose a polygon OABCDEO. Side![]() are taken in same order and side
are taken in same order and side ![]() is taken in opposite order.
is taken in opposite order.
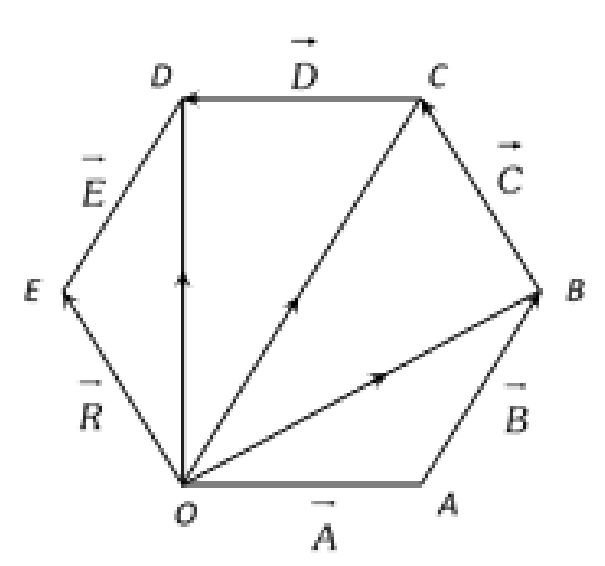
Than according to the polygon law of vector addition

- Scalar Product or Dot product of two vectors:-
Scalar product is defined as the product of the magnitude of two vectors and the cosine of the angle between them. If A and B are two vectors inclined at an angle θ, then scalar product is given by

Properties of dot products:-
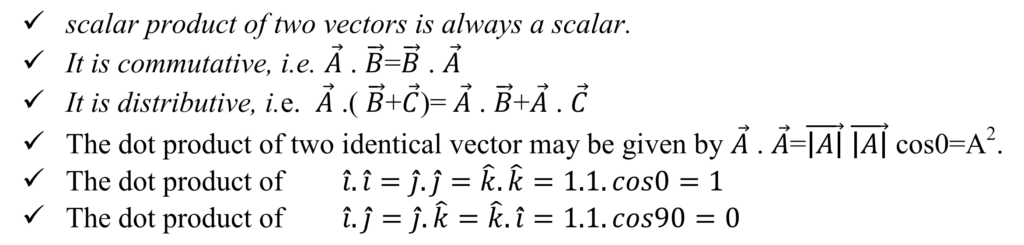
Dot product in term of Cartesian coordinate system
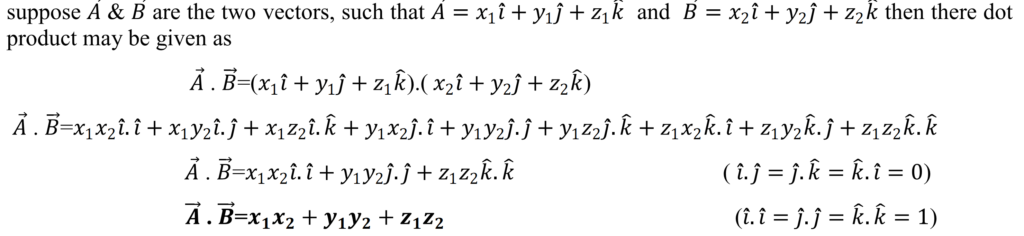
QUESTION 19: The work done by a force ![]() during a displacement r is given by
during a displacement r is given by
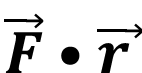
. Suppose a force of 12 N acts on a particle in vertically upward direction and the particle is displaced through 2.0 m in vertically downward direction. Find the work done by the force during this displacement.
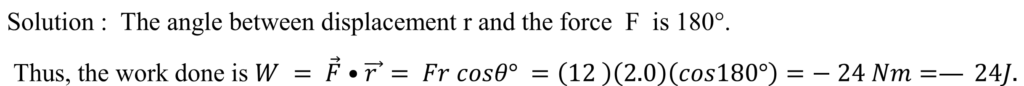
QUESTION 20: The vector ![]() has a magnitude of 5 unit,
has a magnitude of 5 unit, ![]() has a magnitude of 6 unit and the cross product of
has a magnitude of 6 unit and the cross product of![]() and has a magnitude of 15 unit. Find the angle between
and has a magnitude of 15 unit. Find the angle between
 and
and 

Question21: suppose ![]() are the two vectors, such that
are the two vectors, such that ![]()
and ![]() then obtain there dot product .
then obtain there dot product .
Question22 : suppose & are the two mutually perpendicular vectors, such that
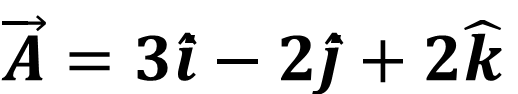 and
and 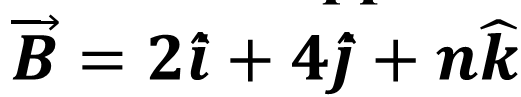 then obtain value of n .
then obtain value of n .
- Vector Product of two vectors or Cross Product of two vectors:-
Vector product is defined as the product of the magnitude of the two vectors and the sine of the angle between them. If A and B are two vectors inclined at an angle θ, then vector product is given by
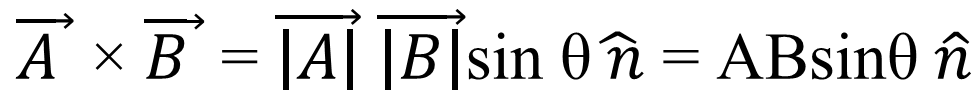
The direction of vector product is given by unit vector perpendicular to the plane containing A and B.
Properties of cross products:-
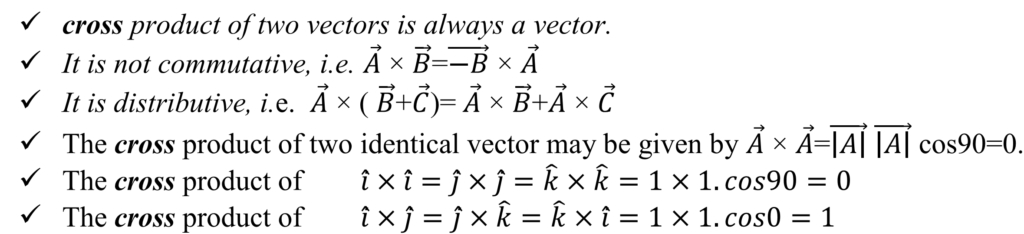
cross product in term of Cartesian coordinate system
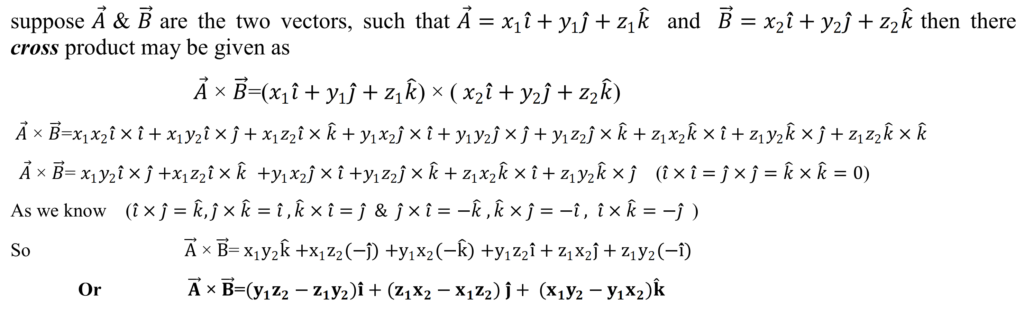
- Rectangular components of a vector.
The process of breaking one vector into two or more vectors is called resolution and the vectors so obtained are called components of the vector.
Consider a vector ![]() inclined to x axis at an angle θ. If
inclined to x axis at an angle θ. If ![]()
are the component of Vector ![]() along x axis and y axis then by parallelogram law
along x axis and y axis then by parallelogram law